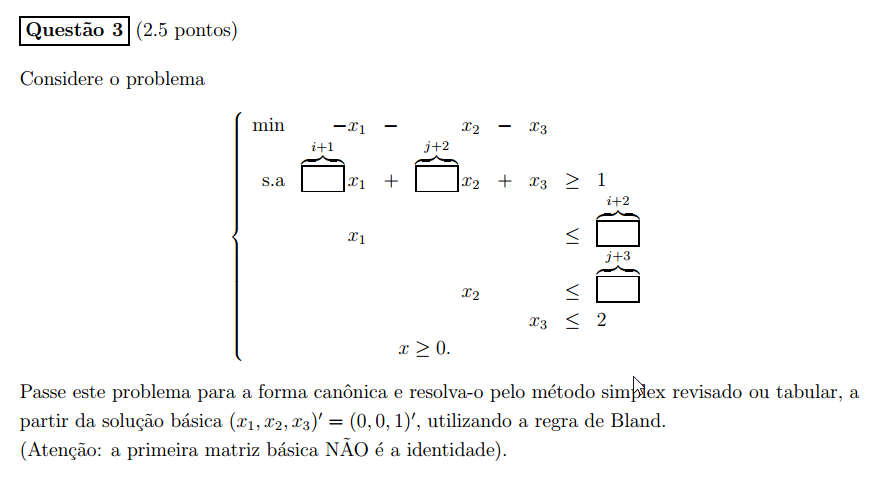
Professor, anexei um print do problema em questão.
Ele pede pra resolver o simplex a partir de uma solução básica, mas eu não entendi como isto ajuda determinar a base inicial.
Professor, anexei um print do problema em questão.
Ele pede pra resolver o simplex a partir de uma solução básica, mas eu não entendi como isto ajuda determinar a base inicial.
Ótima questão, Felipe! De fato isso está plenamente dentro da matéria vista, e algo parecido poderia cair na prova. Isso não tem a ver com o "algoritmo de inicialização" do simplex, que ainda não vimos, mas sim com a relação entre bases (conjuntos de índices) e soluções básicas associadas (através de restrições ativas).
Os resultados das notas de aula mais diretamente relacionados com essa questão são o teorema 2.4 e o exercício 2.5. A primeira coisa portanto é passar o problema para a forma canônica, pois o conceito de bases só existe neste contexto e com a hipótese fundamental (A tem linhas l.i.); a hipótese fundamental será satisfeita trivialmente neste caso pois o problema na forma canônica tem uma identidade associada às variáveis residuais (x4,x5,x6,x7). O ponto x=(0,0,1)' do poliedro original corresponde ao ponto x=(0,0,1,0,i+2,j+3,1)' na forma canônica (basta substituir os valores x1=0, x2=0, x3=1 no sistema de equações Ax=b com as variáveis residuais).
Pelo exercício 2.4, para sabermos que x=(0,0,1,0,i+2,j+3,1)' é mesmo um vértice, basta verificar que ele é viável e que as colunas A3,A5,A6,A7 associadas a xj!=0 são l.i.. O teorema 2.4 nos garante que existe uma base B={b1,b2,b3,b4} associada a este vértice, e esta base tem que conter os índices {3,5,6,7} (pois os índices não-básicos sempre correspondem a componentes xj=0). Portanto essa é a base inicial para o problema, e para aplicar o simplex revisado basta achar a matriz inversa de [A3|A5|A6|A7] (que não é a identidade, conforme a dica da questão).
Neste exemplo os índices da base são determinados univocamente pelo ponto x, pois este é um vértice não-degenerado que possui exatamente m=4 componentes não-nulas. Numa outra questão parecida, poderia acontecer dos índices xj!=0 não chegarem a m: nesse caso o vértice seria degenerado, e consequentemente a base teria que ser completada incluindo-se alguns índices com xj=0. A única preocupação com essa escolha de quais índices com xj=0 seriam escolhidos é garantir que o conjunto de m colunas resultante seja l.i. e de fato corresponda a uma base. Depois disso, o simplex poderia ser aplicado normalmente.
Marcelo
Não tinha pego a ideia de transformar o ponto do PL original no equivalente do PLC com (0 0 1 0 i+2 j+3 1).
Obrigado, professor!
Abs.