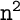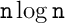Ois,
Excelente discussão!
fui atrás de ver a API do Array.sort() com o Andrew e entendi que como o número de comparações feito por ele é proporcional a nlogn e o meu método de comparação é linear em n [...] Isso faz sentido?
Tudo que vocês pensaram faz sentido.
Arrays.sort() se apoio no compareTo() do objeto.
Em comparação de strings o que pega é o número de vezes que examinamos um caractere (charAt()).
Cada vez Arrays.sort() compara strings examina os seus prefixos.
Assim, uma simples comparação de chaves com prefixos comuns longos acaba custando muiiitoo caro.
Esse custo pode ser proporcional a n, no caso aesop-2copies.txt chega a ser n/2.
O ponto é: algoritmos genéricos examinam um mesmo caractere (charAt()) várias vezes.
Como discutimos ontem, LSD compara cada caractere ums vez e o consumo de tempo é proporcional a nW, onde W é o comprimento das palavras. O Espaço extra é n + R.
No caso de ordenação de sufixos circulares o consumo de tempo é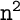 
, enquanto o tamanho da entrada é n. Assim, o consumo de tempo de LSD é quadrático.
Já MSD tem um comportamento de pior caso (com prefixos comuns longos) nW mais um sobrepeso de espaço extra proporcional a n + D x R onde D é a profundidade da recursão. O loop interno de MSD é meio pesado: ordenação por contagem.
Entretanto, em geral, para textos típos, MSD deve ter um compartamento sublinear: nem todo caractere das strings é examinado.
Bruna, você tem razão, aesop-2copies.txt, aesop-4copies.txt ... não são textos típico. É sacanagem. Mas, apesar de ser sacanagem, chama a atençaõ para questões interessantes (e ajudou a corrigir um problema na sua implementação original).
Dos algoritmo que conversamos, para textos típicos, 3-way string (radix) quicksort funciona muito bem. Esse algoritmo é, digamos, da família MSD. Para o EP de vocês, uma implementação adaptada da classe Quick3string de SW, como a Bruna sugere, tem um desempenho excelente.
Por fim, conversamos rapidamente sobre a ideia central dos algoritmos da família prefix-doubling. O algoritmo que executamos ontem na aula é dessa família e seu consumo de tempo é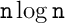 
. Por isso ele é muito rápido, inclusive com textos como aesop-2copies.txt e aesop-4copies.txt.
Como o Nathan falou para a Bruna, há muuuiittoo material sobre ordenação de sufixos. Coloquei com as notas de aula uma cópia do artigo A Taxonomy of Suffix Array Construction Algorithms. Nesse artigo os autores classificam vários algoritmos para ordenação de sufixos. Em particular sobre prefix-doubling algorithms eles atribuem a ideia original a Karp, Miller e Rosenberg (1972). Eles dizem que há dois prefix-doubling algorithms principais:
- Manber e Myers (1993) que usa prefix-doubling com uma política
MSD e
- Larsson e Sadakane (1999) que usa prefix-doubling com 3-way (radix) quicksort de Bentley e McIlroy (1993).
O programa que executei na aula é uma implementação do algoritmo de Larsson e Sadakane.
Pausa para os comerciais: Richard Karp é um nome que vocês verão muito quando estudarem complexidade computacional. Vocês verão um pouquinho de complexidade computacional em Análise de Algoritmos. Mas realmente, para entender melhor essas coisa, seria legal cursar MAC0414 Autômatos, Computabilidade e Complexidade. Essa disciplina será oferecida no próximo semestre, Bem, eu acho essas coisas legais, mas aqui tem o meu viés teórico. Fim do comercial.
Posso dormir em paz?
Sempre.
Tudo é uma questão de manter.
A mente quieta.
A espinha ereta.
E o coração tranquilo.
Leila Pinheiro