Oi pessoal,
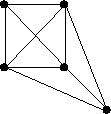
Uma questão que ficou suspensa algumas aulas atrás e que estava me intrigando era encontrar um grafo que não pudesse ser o grafo das arestas de outro.
Acho que finalmente achei um exemplo, mas não tenho certeza se está correto.
Humm.
Acho que não.
(Mas posso estar errado.)
Acho que não.
(Mas posso estar errado.)
Depois eu penso melhor no seu exemplo.
Mas uma maneira de construir um exemplo para isso e mostrar que o grafo realmente não é o grafo das arestas de outro é usar propriedades que você conhece do grafo das arestas.
Pelo teorema de Vizing, temos que o índice cromático (menor número de "cores" com as quais você consegue colorir as arestas de um grafo) é menor ou igual ao grau máximo deste grafo mais 1.
Já mostramos ainda que o índice cromático de um grafo dado é igual ao número cromático de seu grafo das arestas. Ainda que o grau máximo de um grafo é igual ao tamanho da clique máxima do grafo das arestas.
Assim se encontrarmos um grafo tal que seu número cromático é estritamente maior que o tamanho do clique máximo mais 1, teremos que esse grafo não pode ser o grafo das arestas de nenhum grafo.
O seu exemplo não tem essa propriedade. Então não conseguimos eliminar a possibilidade dele ser o grafo das arestas de outro grafo com esse critério. Mas isso não quer dizer que ele realmente não seja.
Existem exemplos de grafos com números cromáticos arbitrariamente maiores do que o tamanho do clique máximo. Mas eu estou com sono e não estou conseguindo pensar em nenhum.
Amanhã eu penso melhor.
Mas uma maneira de construir um exemplo para isso e mostrar que o grafo realmente não é o grafo das arestas de outro é usar propriedades que você conhece do grafo das arestas.
Pelo teorema de Vizing, temos que o índice cromático (menor número de "cores" com as quais você consegue colorir as arestas de um grafo) é menor ou igual ao grau máximo deste grafo mais 1.
Já mostramos ainda que o índice cromático de um grafo dado é igual ao número cromático de seu grafo das arestas. Ainda que o grau máximo de um grafo é igual ao tamanho da clique máxima do grafo das arestas.
Assim se encontrarmos um grafo tal que seu número cromático é estritamente maior que o tamanho do clique máximo mais 1, teremos que esse grafo não pode ser o grafo das arestas de nenhum grafo.
O seu exemplo não tem essa propriedade. Então não conseguimos eliminar a possibilidade dele ser o grafo das arestas de outro grafo com esse critério. Mas isso não quer dizer que ele realmente não seja.
Existem exemplos de grafos com números cromáticos arbitrariamente maiores do que o tamanho do clique máximo. Mas eu estou com sono e não estou conseguindo pensar em nenhum.
Amanhã eu penso melhor.