EP6 - Par Mais Próximo

Objetivos

Neste ponto você já sabe mais sobre análise de consumo de tempo do que sabia no início do semestre. Você viu funções como merge_sort() e quick_sort() que são exemplos clássicos, especialmente o primeiro, da estratégia de Divisão e Conquista. Neste exercício programa você comprovará o poder dessa estratégia solucionando um problema geométrico.

Problema

No problema do par mais próximo (closest pair problem), queremos encontrar dois pontos de uma coleção dada tais que a distância entre eles seja a menor possível. Uma aplicação prática deste problema, na sua versão cinética, é em controle de tráfego aéreo: os dois aviões que estão em maior perigo de colisão são aqueles que estão mais próximos.

Problema do par mais próximo. Dada uma lista de pontos do plano, encontrar dois pontos (distintos) da lista tais que a distância entre eles seja a menor possível.

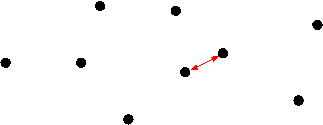
Os pontos dados podem estar em um espaço de dimensão arbitrária, mas neste EP discutiremos o caso em que os pontos estão no plano e a distância entre eles é a euclidiana. Assim, se p0=[x0, y0] e p1=[x1, y1] são (as coordenadas de) dois pontos do plano, a distância entre eles, denotada por distancia(p0, p1), é o número √(x1 − x0)2 + (y1 − y0)2 .

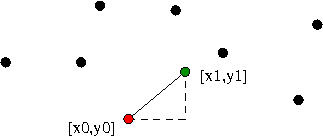
Cada ponto será representado por uma lista [x,y] onde x é a sua abscissa e y é a sua ordenada.

Solução à la MAC0110

A primeira ideia para a resolução do problema do par mais próximo é simplesmente calcularmos a distância entre cada par de pontos, enquanto mantemos a menor distância encontrada até o momento. No EP6 essa ideia será implementada na função mac0110().

Solução à la MAC0122

Como você viu com as funções quadráticas para ordenação de listas buble_sort(), selecao(), insercao(), quando o tamanho da entrada é dobrado, o consumo de tempo é aumentado por um fator de quatro. Por outro lado, também é verdade que se o tamanho da entrada é dividido pela metade o consumo de tempo diminui por um fator de quatro. A divisão da entrada na metade é a chave da eficiência da estratégia de Divisão e Conquista para o problema do par mais próximo.

Neste EP você implementará uma função mac0122() que é muito semelhante ao merge_sort(). Essa função, que passamos a descrever, corresponde a uma pequena simplificação do algoritmo desenvolvido por M.I. Shamos and D. Hoey em 1975.

A função mac0122() recebe uma lista de pontos ordenados da esquerda para a direita. Com isso, temos uma representação dos pontos ordenados em relação às suas coordenadas x (= abscissas). Isso significa, que a função exige um pré-processamento dos pontos.

Como o merge_sort() a função mac0122() é recursiva e além de uma lista de pontos lista_pontos recebe dois inteiros p0 e p1. A função deve retornar um float d e uma lista [p0,p1] com um par de pontos que são a solução do problema do para mais próximo para a lista_pontos[p:r]:

• d é a menor distância entre dois pontos em lista_pontos[p:r] e
• p0 e p1 são pontos em lista_pontos[p:r] que estão a distância d.

Na base da recursão, se a lista tem poucos pontos, o problema é resolvido diretamente. Caso contrário, a ideia é, em cada nível da recursão, executar as três fases a seguir.

Dividir

De maneira idêntica a função merge_sort(), calcule o índice q do ponto central da lista.

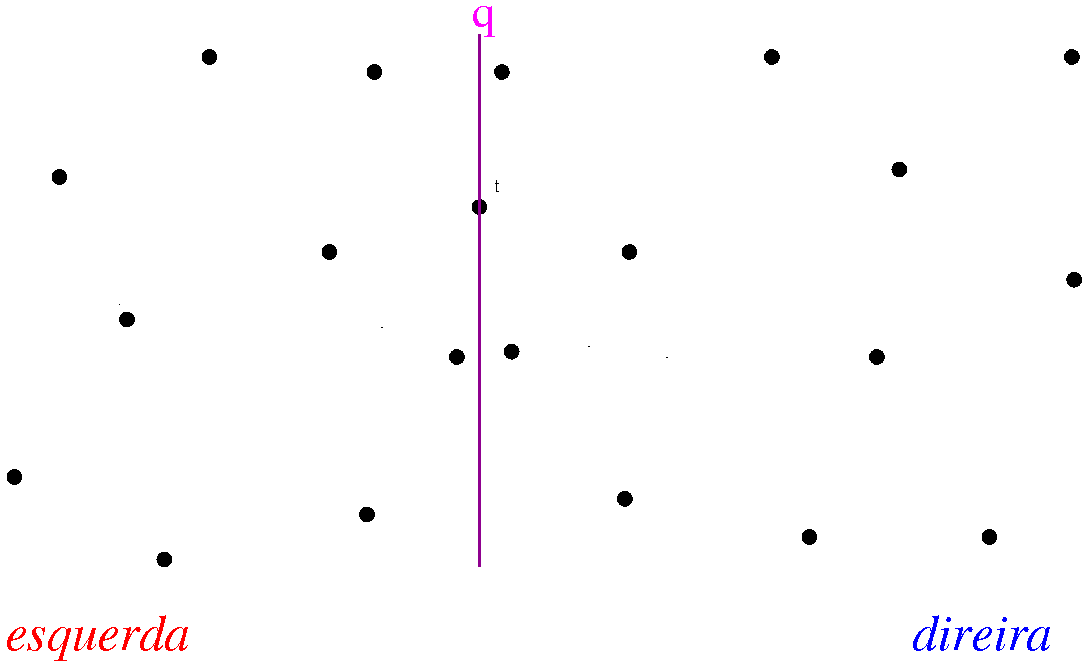
Conquistar

determine, recursivamente, a menor distância d_esq entre um par de pontos [p0_esq,p1_esq] da esquerda e a menor distância d_dir entre um par de pontos [p0_dir,p1_dir] de dois pontos da direita.

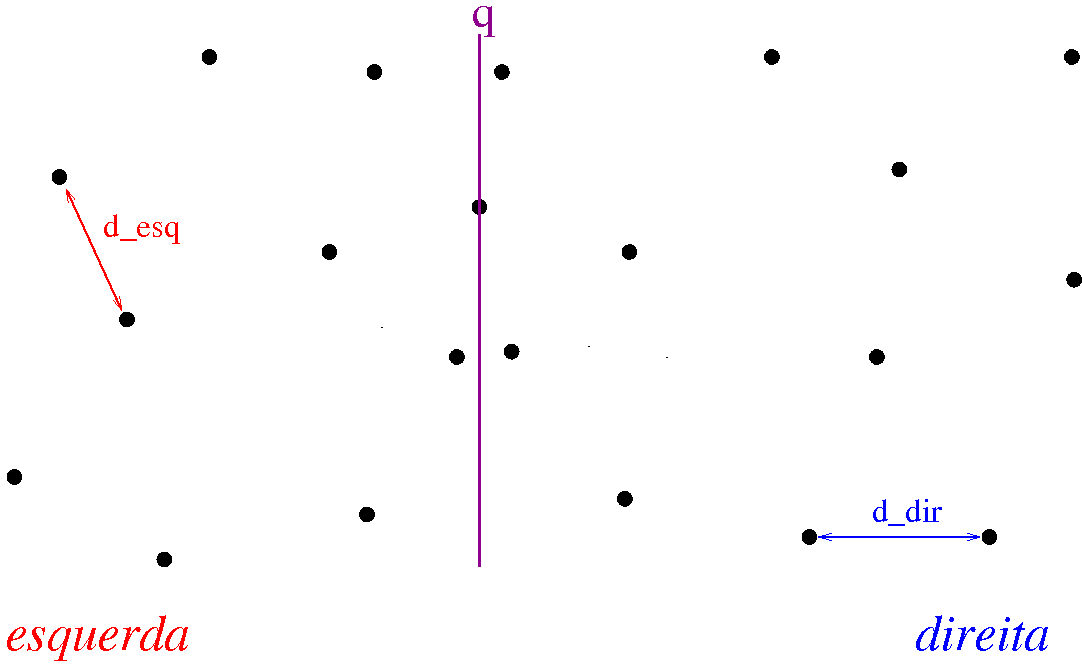
Combinar

Retorne o mínimo entre d_esq, d_dir e a menor distância d_faixa entre um ponto da esquerda e um ponto da direita e o correspondente par de pontos.

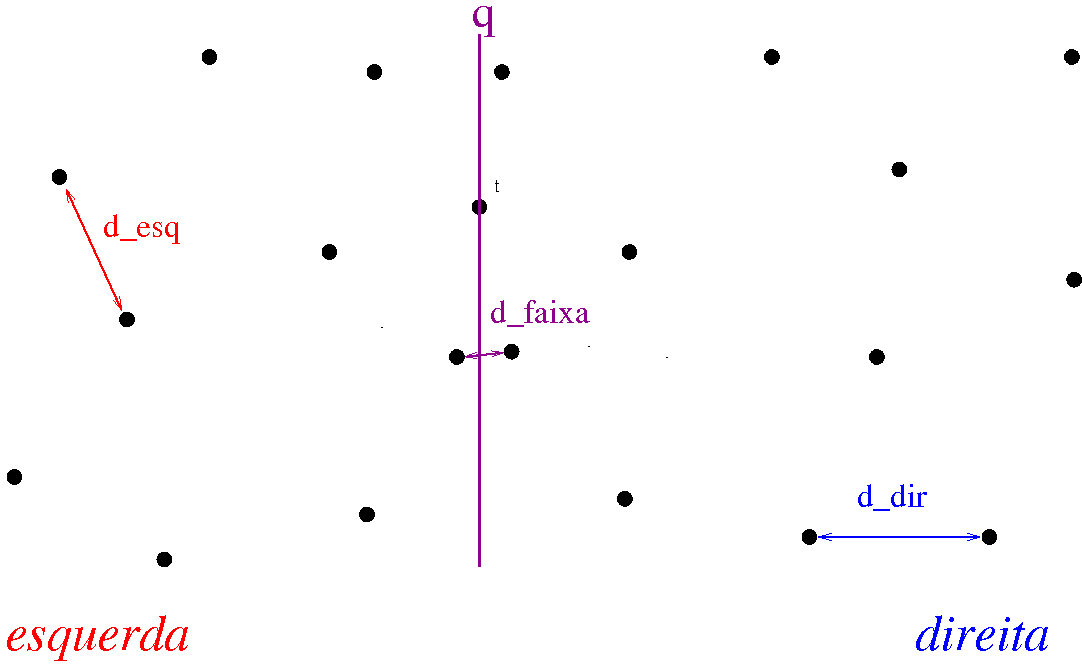
A fase combinar é o coração da função mac0122(), da mesma forma que a função intercale() é o coração do merge_sort(). Essa fase é essencialmente implementada no EP através da função para_mais_proximo_faixa(). Uma implementação ingênua dessa função calcularia a distância entre cada ponto de lista_pontos[p:q] e cada ponto de lista_pontos[q:r] a fim de determinar a menor dessas distância d_faixa e o correspondente par de pontos [p0_faixa,p1_faixa].

A observação chave aqui é que não é necessário que a função par_mais_proximo_faixa() calcule a distância entre pontos que estão sabidamente a uma distância maior que d = min(d_esq,d_dir). Assim, basta par_mais_proximo_faixa() calcular a distância entre os pontos em lista_pontos[p,q] e lista_pontos[q,r] que estão a uma distância menor que d da reta vertical x=lista_pontos[q][0]. Chamaremos essa região de faixa de largura d em relação a q

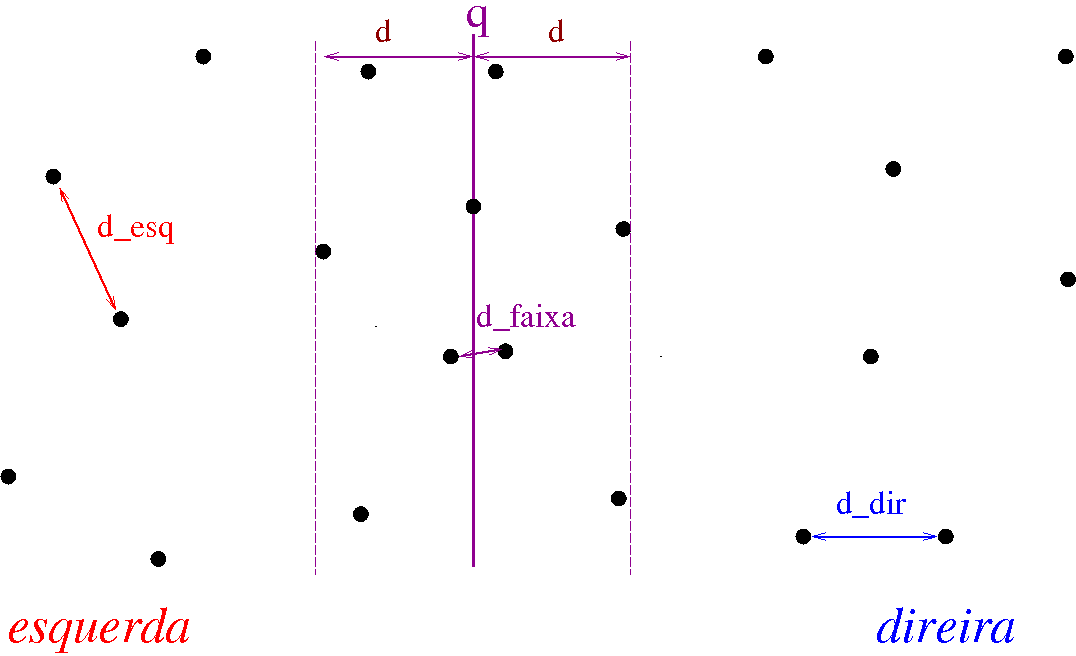
Finalmente, em cada nível da recursão, após par_mais_proximo_faixa() ter feito o seu serviço, mac0122() tem em mãos d_esq, d_faixa e d_dir, e os respectivos pares. A última tarefa que mac0122() deve então fazer é retornar a menor dentre essas três e o par de pontos correspondente.

O que você deve fazer

Neste EP6 você implementará quatro funções. São elas

• distancia();
• mac0110();
• par_mais_proximo_faixa(); e
• mac0122().

A função main() está completamente implementada. As especificações dessas funções estão no arquivo esqueleto_ep6.py.

Exemplos de execução do programa

O que aparece em vermelho foi digitado pelo usuário.

Exemplo 0

no. de pontos >>> 128
semente >>> 0
função ('0' para mac0110, '1' para mac0122) >>> 0

gere_pontos(): gerando 128 pontos ...
gere_pontos(): pontos gerados.

Resultado: 
  par mais próximo  = [[623, 689], [621, 686]]
  menor distância   = 3.61
  tempo de execução = 0.01s

executar animação ('s' para sim, 'n' para não) >>> n
Fui!

Exemplo 1

no. de pontos >>> 256
semente >>> 0
função ('0' para mac0110, '1' para mac0122) >>> 0

gere_pontos(): gerando 256 pontos ...
gere_pontos(): pontos gerados.

Resultado: 
  par mais próximo  = [[623, 689], [621, 686]]
  menor distância   = 3.61
  tempo de execução = 0.04s

executar animação ('s' para sim, 'n' para não) >>> n   
Fui!

Exemplo 2

no. de pontos >>> 512
semente >>> 0
função ('0' para mac0110, '1' para mac0122) >>> 0

gere_pontos(): gerando 512 pontos ...
gere_pontos(): pontos gerados.

Resultado: 
  par mais próximo  = [[-404, 420], [-405, 423]]
  menor distância   = 3.16
  tempo de execução = 0.15s

executar animação ('s' para sim, 'n' para não) >>> n
Fui!

Exemplo 3

no. de pontos >>> 1024
semente >>> 0
função ('0' para mac0110, '1' para mac0122) >>> 0

gere_pontos(): gerando 1024 pontos ...
gere_pontos(): pontos gerados.

Resultado: 
  par mais próximo  = [[-960, 459], [-962, 459]]
  menor distância   = 2.00
  tempo de execução = 0.57s

executar animação ('s' para sim, 'n' para não) >>> n
Fui!

Exemplo 4

no. de pontos >>> 128
semente >>> 0
função ('0' para mac0110, '1' para mac0122) >>> 1

gere_pontos(): gerando 128 pontos ...
gere_pontos(): pontos gerados.

execute(): pontos sendo ordenados em relação a coordenada x...
execute(): pontos ordenados.

Resultado: 
  par mais próximo  = [[621, 686], [623, 689]]
  menor distância   = 3.61
  tempo de execução = 0.00s

executar animação ('s' para sim, 'n' para não) >>> n
Fui!

Exemplo 5

no. de pontos >>> 256
semente >>> 0
função ('0' para mac0110, '1' para mac0122) >>> 1

gere_pontos(): gerando 256 pontos ...
gere_pontos(): pontos gerados.

execute(): pontos sendo ordenados em relação a coordenada x...
execute(): pontos ordenados.

Resultado: 
  par mais próximo  = [[621, 686], [623, 689]]
  menor distância   = 3.61
  tempo de execução = 0.00s

executar animação ('s' para sim, 'n' para não) >>> n
Fui!

Exemplo 6

no. de pontos >>> 512
semente >>> 0
função ('0' para mac0110, '1' para mac0122) >>> 1

gere_pontos(): gerando 512 pontos ...
gere_pontos(): pontos gerados.

execute(): pontos sendo ordenados em relação a coordenada x...
execute(): pontos ordenados.

Resultado: 
  par mais próximo  = [[-405, 423], [-404, 420]]
  menor distância   = 3.16
  tempo de execução = 0.01s

executar animação ('s' para sim, 'n' para não) >>> n
Fui!

Exemplo 7

no. de pontos >>> 1024
semente >>> 0
função ('0' para mac0110, '1' para mac0122) >>> 1

gere_pontos(): gerando 1024 pontos ...
gere_pontos(): pontos gerados.

execute(): pontos sendo ordenados em relação a coordenada x...
execute(): pontos ordenados.

Resultado: 
  par mais próximo  = [[-962, 459], [-960, 459]]
  menor distância   = 2.00
  tempo de execução = 0.02s

executar animação ('s' para sim, 'n' para não) >>> n
Fui!

Roteiro

• Faça o download dos arquivos esqueleto_ep6.py. util.py e console.py.

• Mude o nome do arquivo esqueleto_ep6.py para NUSP_ep6.py, onde o NUSP é o seu número USP.

• Abra o esqueleto no Spyder ou em qualquer outro editor ou ambiente apropriado para desenvolver programas em Python. Esse será o único arquivo que você deve editar.

• Leia e preencha o cabeçalho com o seu nome, nusp, etc. Não modifique o resto do cabeçalho.

• Execute o arquivo para ver se está tudo ok. O programa deve imprimir:

  no. de pontos >>> 128
  semente >>> 0
  função ('0' para mac0110, '1' para mac0122) >>> 0
  
  gere_pontos(): gerando 128 pontos ...
  gere_pontos(): pontos gerados.
  Vixe! Ainda não fiz a função mac0110().
  
  Resultado: 
    par mais próximo  = []
    menor distância   = None
    tempo de execução = 0.00s
  
  executar animação ('s' para sim, 'n' para não) >>> n
  Fui!

• Antes de escrever cada função, leia atentamente a especificação da função e os exemplos.

• Teste cada função separadamente das demais usando o console do Spyder (= Python Shell ou IPython). Você também pode usar para os testes um terminal.

• Teste o EP6 completo, chamando agora a função main(), inclusive com outros exemplos além dos fornecidos.

• Após testar o seu programa com vários exemplos, entregue o arquivo NUSP_ep6.py.

• Não deixe de seguir as Instruções para entrega de EPs.

Entrega

A primeira entrega deve ser feita até o dia 06/10 (até 23h55m).
O EP receberá comentários no dia 07/10.
Uma nova versão poderá ser entregue até o dia 09/10 10/10 (até 23h55m).